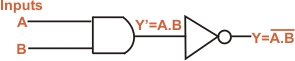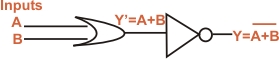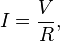Truth Table :
Wednesday, April 30, 2014
Sunday, April 27, 2014
Schematic and Truth Table ( LOGIC GATES)
LOGIC GATES
schematic diagram
- is a representation of the elements of a system using abstract, graphic symbols rather than realistic pictures. A schematic usually omits all details that are not relevant to the information the schematic is intended to convey, and may add unrealistic elements that aid comprehension. (http://en.wikipedia.org/wiki/Schematic)
truth table
- is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their logical variables (Enderton, 2001). (http://en.wikipedia.org/wiki/Truth_table)
Logic Gates with Truth Table
AND gate
74 Series Logic IC Datasheets :
(http://www.skot9000.com/ttl/)
- AND - True if A and B are both True
- OR - True if either A or B are True
- NOT - Inverts value: True if input is False; False if input is True
- XOR - True if either A or B are True, but False if both are True
- NAND - AND followed by NOT: False only if A and B are both True
- NOR - OR followed by NOT: True only if A and B are both False
- XNOR - XOR followed by NOT: True if A and B are both True or both False
schematic diagram
- is a representation of the elements of a system using abstract, graphic symbols rather than realistic pictures. A schematic usually omits all details that are not relevant to the information the schematic is intended to convey, and may add unrealistic elements that aid comprehension. (http://en.wikipedia.org/wiki/Schematic)
truth table
- is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their logical variables (Enderton, 2001). (http://en.wikipedia.org/wiki/Truth_table)
Logic Gates with Truth Table
AND gate

- The AND gate is an electronic circuit that gives a high output (1) only if all its inputs are high. A dot (.) is used to show the AND operation i.e. A.B. Bear in mind that this dot is sometimes omitted i.e. AB

- The OR gate is an electronic circuit that gives a high output (1) if one or more of its inputs are high. A plus (+) is used to show the OR operation.
NOT gate
- The NOT gate is an electronic circuit that produces an inverted version of the input at its output. It is also known as an inverter. If the input variable is A, the inverted output is known as NOT A. This is also shown as A', or A with a bar over the top, as shown at the outputs. The diagrams below show two ways that the NAND logic gate can be configured to produce a NOT gate. It can also be done using NOR logic gates in the same way.

- This is a NOT-AND gate which is equal to an AND gate followed by a NOT gate. The outputs of all NAND gates are high if any of the inputs are low. The symbol is an AND gate with a small circle on the output. The small circle represents inversion.
- This is a NOT-OR gate which is equal to an OR gate followed by a NOT gate. The outputs of all NOR gates are low if any of the inputs are high.
- The symbol is an OR gate with a small circle on the output. The small circle represents inversion.
- The 'Exclusive-OR' gate is a circuit which will give a high output
if either, but not both, of its two inputs are high. An encircled
plus sign (
 ) is used to show the EOR operation.
) is used to show the EOR operation.
NAND gate

NOR gate
EXOR gate
EXNOR gate
(http://www.ee.surrey.ac.uk/Projects/CAL/digital-logic/gatesfunc/index.html)The 'Exclusive-NOR' gate circuit does the opposite to the EOR gate. It will give a low output if either, but not both, of its two inputs are high. The symbol is an EXOR gate with a small circle on the output. The small circle represents inversion.
74 Series Logic IC Datasheets :
| part # | description |
| 74LS00 | Quad 2-Input NAND Gate |
| 74LS01 | Quad 2-Input NAND Gate; Open Collector Outputs |
| 74LS02 | Quad 2-Input NOR Gate |
| 74LS03 | Quad 2-Input NAND Gate; Open Collector Outputs |
| 74LS04 | Hex Inverter |
| 74LS05 | Hex Inverter; Open Collector Outputs |
| 74LS06 | Hex Inverter; Open Collector High Voltage Outputs |
| 74LS07 | Hex Buffer; Open Collector High Voltage Outputs |
| 74LS08 | Quad 2-Input AND Gate |
| 74LS09 | Quad 2-Input AND Gate; Open Collector Outputs |
| 74LS10 | Triple 3-Input NAND Gate |
| 74LS11 | Triple 3-Input AND Gate |
| 74LS12 | Triple 3-Input NAND Gate; Open Collector Outputs |
| 74LS13 | Dual 4-Input NAND Schmitt Triggers |
| 74LS14 | Hex Schmitt-Trigger Inverter |
| 74LS15 | Triple 3-Input AND Gate; Open Collector Outputs |
| 74LS16 | Hex Inverter; Open Collector 15V Outputs |
| 74LS17 | Hex Driver; Open Collector 15V Outputs |
| 74LS19 | NAND Schmitt Trigger; Totem Pole Output |
| 74LS20 | Dual 4-Input NAND Gate |
| 74LS21 | Dual 4-Input AND Gate; Open Collector Outputs |
| 74LS22 | Dual 4-Input NAND Gate; Open Collector Outputs |
| 74LS23 | 2x Four input NOR with Strobe |
| 74LS25 | 2x Four input NOR with Strobe |
| 74LS26 | Quad 2-Input NAND Gate; OC (15V) |
| 74LS27 | Triple 3-Input NOR Gate |
| 74LS28 | Quad 2-Input NOR Gates |
| 74LS30 | 8-Input NAND Gate |
| 74LS31 | Delay Element |
| 74LS32 | Quad 2-Input OR Gate |
| 74LS33 | Quad 2-Input NOR Gate; Open Collector Outputs |
| 74LS37 | Quad 2-Input NAND Gates |
| 74LS38 | Quad 2-Input NAND Gates; Open Collector Outputs |
| 74LS39 | 4x Two input NAND, Open collector |
| 74LS40 | Dual 4-Input NAND Gates |
| 74LS42 | BCD to DECIMAL Decoder |
| 74LS45 | Four-to-Ten (BCD to Decimal) DECODER, High current |
| 74LS46 | BCD to Seven-Segment DECODER, Open Collector, lamp test and leading zero handling |
| 74LS47 | BCD to 7-Segment Decoder; Open Collector Outputs (15V) |
| 74LS48 | BCD to 7-Seg Decoder; Outputs Active high |
| 74LS49 | BCD to 7-Seg Decoder-Outputs Active High |
| 74LS50 | 2x (Two input AND) NOR (Two input AND), expandable |
| 74LS51 | Dual AND-OR-INVERT Gates |
| 74LS53 | NOR of Four Two input ANDs, expandable |
| 74LS54 | 4-Wide AND-OR-INVERT Gate |
| 74LS55 | 4-Wide; 2-Input AND-OR-INVERT Gate |
| 74LS56 | Frequency Divider |
| 74LS57 | Frequency Divider |
| 74LS64 | 4-3-2-2 AND-OR-INVERT |
| 74LS65 | 4-3-2-2 AND-OR-INVERT |
| 74LS68 | Dual 4-Bit Decade or Binary Counter |
| 74LS69 | Dual 4-Bit Decade or Binary Counter |
| 74LS70 | 1x gated JK FLIPFLOP with preset and clear |
| 74LS72 | 1x gated JK FLIPFLOP with preset and clear |
| 74LS73 | Dual J-K Flip-Flop |
| 74LS74 | Dual D-Type Flip-Flop |
| 74LS75 | Dual 2-Bit D-Type Flip-Flop |
| 74LS76 | Dual J-K Flip-Flop |
| 74LS77 | 4-Bit D-Type Latch |
| 74LS78 | Dual J-K Flip-Flop |
| 74LS83 | 4-Bit Full Adder |
| 74LS85 | 4-Bit Comparator |
| 74LS86 | Quad Exclusive OR Gate |
| 74LS90 | Decade Counter |
| 74LS91 | 8-Bit Shift Register |
| 74LS92 | Divide-By-12 Counter |
| 74LS93 | 4-Bit Binary Counter |
| 74LS94 | Four bit SHIFT register |
| 74LS95 | 4-Bit Shift Register with Parallel Inputs and Outputs |
| 74LS96 | 5-Bit Shift Register with Parallel Inputs and Outputs |
| 74LS107 | Dual J-K Master Slave Flip-Flop |
| 74LS109 | Dual J-K Flip-Flop |
| 74LS112 | Dual J-K Flip-Flop with Preset and Clear |
| 74LS113 | Dual J-K Flip-Flop |
| 74LS114 | Dual J-K Flip-Flop |
| 74LS116 | 2x Four bit LATCH with clear |
| 74LS121 | Monostable Multivibrator |
| 74LS122 | Retriggerable Monostable Multivibrator |
| 74LS123 | Retriggerable Monostable Multivibrator |
| 74LS124 | 2x Clock Generator or Voltage Controlled Oscillator |
| 74LS125 | Quad Line Driver; 3-State Outputs |
| 74LS126 | Quad Line Driver; 3-State Outputs |
| 74LS128 | 4x Two input NOR, Line driver |
| 74LS130 | Retriggerable Monostable Multivibrator |
| 74LS132 | Quad 2-Input NAND Schmitt Trigger |
| 74LS133 | 13-Input NAND Gate |
| 74LS134 | Twelve input NAND, Tri-state |
| 74LS135 | 4x Two input XOR (exclusive or) |
| 74LS136 | Quad 2-Input Exclusive OR Gates |
| 74LS137 | 3-Line to 8-Line Demultiplexer with Address Latch |
| 74LS138 | 3-Line to 8-Line Demultiplexer |
| 74LS139 | 2-Line to 4-Line Decoder/Demultiplexer |
| 74LS140 | 2x Four input NAND, 50 ohm Line Driver |
| 74LS143 | Four bit counter and latch with 7-segment LED driver |
| 74LS145 | BCD to Decimal Decoder/Driver |
| 74LS147 | 10-Line to 4-Line Priority Encoder |
| 74LS148 | 8-Line to 3-Line Priority Encoder |
| 74LS150 | 16-1 SELECTOR (multiplexer) |
| 74LS151 | 8-Line to 1-Line Multiplexer |
| 74LS153 | Dual 4-Line to 1-Line Multiplexer |
| 74LS154 | 4-Bit Binary Decoder/Demultiplexer |
| 74LS155 | Dual 2-Bit Binary Decoders/Demultiplexer |
| 74LS156 | Dual 2-Bit Binary Decoders/Demultiplexer |
| 74LS157 | Quad 2-Line to 1-Line Multiplexer |
| 74LS158 | Quad 2-Line to 1-Line Multiplexer |
| 74LS159 | 4-16 DECODER (demultiplexer), Open collector |
| 74LS160 | 4-Bit Synchronous Programmable Counter |
| 74LS161 | 4-Bit Synchronous Programmable Counter |
| 74LS162 | 4-Bit Synchronous Programmable Counter |
| 74LS163 | 4-Bit Synchronous Programmable Counter |
| 74LS164 | 8-Bit Shift Register with Parallel Outputs |
| 74LS165 | 8-Bit Shift Register with Parallel Inputs |
| 74LS166 | 8-Bit Shift Register with Parallel Inputs |
| 74LS168 | Up/Down 4-Bit Synchronous Counter |
| 74LS169 | Up/Down 4-Bit Synchronous Counter |
| 74LS170 | 16-Bit RAM; Open Collector Outputs |
| 74LS173 | 4-Bit Quad D-Type Flip-Flops; 3-State Outputs |
| 74LS174 | Hex D-Type Flip-Flop |
| 74LS175 | Quad D-Type Flip-Flop |
| 74LS180 | Four bit parity checker |
| 74LS181 | 4-bit Arithmetic Logic Unit |
| 74LS182 | Look Ahead Carry Generator |
| 74LS183 | Dual Carry-Save Full Adder |
| 74LS190 | Synchronous Up/Down Decade Counter |
| 74LS191 | Synchronous Up/Down 4-Bit Binary Counter |
| 74LS192 | Synchronous Up/Down Decade Counter |
| 74LS193 | Synchronous Up/Down 4-Bit Binary Counter |
| 74LS194 | 4-Bit Bidirectional Shift Register |
| 74LS195 | 4-Bit Parallel-Access Shift Register |
| 74LS196 | Programmable Decade Counter |
| 74LS197 | Programmable Decade Counter |
| 74LS198 | Eight bit parallel in and out bidirectional SHIFT register |
| 74LS199 | Eight bit parallel in and out bidirectional SHIFT register, JK serial input |
| 74LS221 | Dual Monostable Multivibrator; Schmitt-Trigger Input |
| 74LS240 | Octal Inverting Buffer/Transciever; 3-State Outputs |
| 74LS241 | Octal Buffer/Transciever; 3-State Outputs |
| 74LS242 | Quad 3-State Bus Transceiver |
| 74LS243 | 4-Bit Bidirectional Bus Driver |
| 74LS244 | Octal 3-State Noninverting Buffer |
| 74LS245 | Octal 3-State Noninverting Bus Transceiver |
| 74LS247 | BCD to 7-Seg Decoder/Display Driver OC (15V) |
| 74LS248 | BCD to 7-Seg Decoder/Display Driver OC (15V) |
| 74LS249 | BCD to 7-Seg Decoder/Display Driver OC (15V) |
| 74LS251 | 8-Line to 1-Line Multiplexer; 3-State Outputs |
| 74LS253 | Dual 4-Input Data Selecttor/Multiplexer 3-State |
| 74LS256 | Dual 4-Bit Addressable Latch |
| 74LS257 | Quad 2-Line to 1-Line Multiplexers; 3-State Outputs |
| 74LS258 | Quad 2-Line to 1-Line Multiplexers; 3-State Outputs |
| 74LS259 | 8-Bit Adressable Latch |
| 74LS260 | Dual 5-Input NOR Gate |
| 74LS266 | Quad Exclusive NOR Gate |
| 74LS269 | 8-BIT BIDIRECTIONAL BINARY COUNTER |
| 74LS273 | Octal D-Type Flip-Flop; Common Clock and Clear |
| 74LS279 | Quad SR-Flip-Flops |
| 74LS280 | 9-Bit Parity checker |
| 74LS283 | 4-Bit Full Adder |
| 74LS290 | 4-Bit Decade/Binary Counter |
| 74LS298 | Quad 2-Line to 1-Line Multiplexers with Latch |
| 74LS299 | 8-Bit Bidirectional Universal Shift Register |
| 74LS322 | 8-Bit Sign-Extend Shift Register |
| 74LS323 | 8-Bit Universal Shift Register with Latch |
| 74LS348 | 8-Line to 3-Line Priority Encoder with 3-State Outputs |
| 74LS352 | Dual 4-Line to 1-Line Multiplexers |
| 74LS353 | Dual 4-Line to 1-Line Multiplexers with 3-State Outputs |
| 74LS365 | Hex Bus Line Drivers |
| 74LS366 | 3-State Hex Line Driver |
| 74LS367 | Hex Bus Line Drivers |
| 74LS368 | Hex Inverting Bus Line Drivers |
| 74LS373 | Octal D-Type Latch |
| 74LS374 | Octal D-Type Flip-Flop |
| 74LS375 | Quad D-Type Latch |
| 74LS377 | Octal D-Type Flip-Flop |
| 74LS378 | Hex D-Type Flip-Flop |
| 74LS379 | Quad D-Type Flip-Flop |
| 74LS386 | Quad 2-Input Exclusive OR Gates |
| 74LS390 | Dual Decade Counters |
| 74LS393 | Dual Decade Counters |
| 74LS395 | 4-Bit Shift Register with 3-State Outputs |
| 74LS398 | Quad 2-Input Register |
| 74LS399 | Quad 2-Input Register |
| 74LS490 | Dual Decade Counter |
| 74LS521 | 8-BIT IDENTITY COMPARATOR |
| 74LS533 | Octal D-Type Transparent Latche |
| 74LS534 | Octal Invering D-Type Flip-Flop |
| 74LS538 | 1-OF-8 DECODER WITH 3-STATE OUTPUTS |
| 74LS540 | 8-Bit Inverting Line Driver |
| 74LS541 | OCTAL BUFFER/LINE DRIVER WITH 3-STATE OUTPUTS |
| 74LS543 | OCTAL REGISTERED TRANSCEIVER, NON-INVERTING, 3-STATE |
| 74LS544 | OCTAL REGISTERED TRANSCEIVER, INVERTING, 3-STATE |
| 74LS568 | 4-BIT BIDIRECTIONAL COUNTERS (WITH 3-STATE OUTPUTS) |
| 74LS569 | 4-Bit Synchronous Counter |
| 74LS574 | 8-Bit D-Type Flip-Flop/Bus Driver |
| 74LS579 | 8-BIT BIDIRECTIONAL BINARY COUNTER (3-STATE) |
| 74LS620 | OCTAL BUS TRANSCEIVER WITH 3-STATE OUTPUTS (INVERTING AND NONINVERTING) |
| 74LS623 | Octal Bus Transcievers |
| 74LS629 | Voltage Controlled Oscilator |
| 74LS640 | Octal Bus Transciever |
| 74LS646 | Octal Bus Transciever |
| 74LS648 | Octal Bus Transciever/Register |
| 74LS657 | OCTAL BIDIRECTIONAL TRANSCEIVER WITH 8-BIT PARITY GENERATOR CHECKER (3-STATE OUTPUTS) |
| 74LS669 | 4-Bit Synchronous Up/Down Counter |
| 74LS670 | 4-By-4 Register File; 3-State Outputs |
| 74LS682 | 8-Bit Magnitude/Identity Comparator |
| 74LS684 | 8-Bit Magnitude Comparators |
| 74LS688 | 8-Bit Magnitude Comparators |
| 74LS748 | 8-Line to 3-Line Priority Encoder |
| 74LS779 | 8-BIT BIDIRECTIONAL BINARY COUNTER (3-STATE) |
| 74LS795 | Octal Buffer with 3-State Outputs |
| 74LS848 | 8-Line to 3-Line Priority Encoder with 3-State Outputs |
| 74LS2245 | 25Ohm Octal Bidirectional Transceiver With 3-State Inputs and Outputs |
| 74LS3893 | QUAD FUTUREBUS BACKPLANE TRANSCEIVER (3 STATE + OPEN COLLECTOR) |
Friday, April 25, 2014
Thursday, April 24, 2014
LOGIC GATES and COMBINATION
logic gates
- is an idealized or physical device implementing a Boolean function; that is, it performs a logical operation on one or more logical inputs, and produces a single logical output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and unlimited fan-out, or it may refer to a non-ideal physical device .
Logic circuits include such devices as multiplexers, registers, arithmetic logic units (ALUs), and computer memory, all the way up through complete microprocessors, which may contain more than 100 million gates. In practice, the gates are made from field-effect transistors (FETs), particularly MOSFETs (metal–oxide–semiconductor field-effect transistors).
logic gates
- is an idealized or physical device implementing a Boolean function; that is, it performs a logical operation on one or more logical inputs, and produces a single logical output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and unlimited fan-out, or it may refer to a non-ideal physical device .
Logic circuits include such devices as multiplexers, registers, arithmetic logic units (ALUs), and computer memory, all the way up through complete microprocessors, which may contain more than 100 million gates. In practice, the gates are made from field-effect transistors (FETs), particularly MOSFETs (metal–oxide–semiconductor field-effect transistors).
| Combination of Basic Logic Gates | ||||||||||||||||||||||||
| The OR, AND and NOT gates are the three basic circuits that make up all digital circuits. We shall discuss a few combinations of theses basic circuits. | ||||||||||||||||||||||||
|
(I) NAND Gate: It is
combination of AND gate is connected to the input of a NOT
gate as shown in Fig. (a). Clearly, the output of a NAND gate
is opposite to the AND gate. This is illustrated in the truth
table for the NAND gate. Note that truth table for NAND gate
is developed by inverting the output of the AND gate.
The Boolean expression for NAND function is
This Boolean expression can
be read as Y = not A . B. TO perform
the Boolean algebra operation, First the input must be AND
and then the inversion is performed. Note that output from
NAND gate is always 1 excepted when all of the input are 1.Fig.
(b) shows the logic symbol for a NAND gate. The title bubble
(small circle) on the right end of the symbol means to invert
the AND.
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Truth
Table of NAND
|
||||||||||||||||||||||||
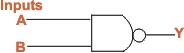
(II)
NOR Gate: It is a combination of OR gate and NOT gate.
In other words, output of OR gate is connected to the input
of a NOT gate as shown in Fig. (c). Note that output of OR
gate is inverted to form NOR gate. This is illustrated in
the truth table for NOR gate. It is clear that truth table
for NOR gate is developed by inverting the outputs of the
OR gate.
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Truth
Table of NOR
|
||||||||||||||||||||||||
|
The Boolean expression for
NOR function is:
The Boolean expression can
be read as Y = not A or B. To perform the Boolean algebra
operation, first the input must be OR and then inversion is
performed. Note that output from a NOR gate is high(1) only
when all the inputs are low (0). If any of the inputs are
high (1) the output is low (0). fig. (d) shows the logic symbol
for a NOR gate. The bubble (small circle) at the Y output
indicates inversion.
| ||||||||||||||||||||||||
Different Types of Resistors
Resistor
- an electric resistor
is a two-terminal passive component specifically used to oppose and
limit current. A resistor works on the principle of Ohm’s Law which
states that voltage across the terminals of a resistor is directly
proportional to the current flowing through it.
Resistor Color Code Information :
Tuesday, April 15, 2014
Ohm's Law
-
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points. Introducing the constant of proportionality, the resistance,one arrives at the usual mathematical equation that describes this relationship:
The law was named after the German physicist Georg Ohm, who, in a treatise published in 1827, described measurements of applied voltage and current through simple electrical circuits containing various lengths of wire. He presented a slightly more complex equation than the one above (see History section below) to explain his experimental results. The above equation is the modern form of Ohm's law.
In physics, the term Ohm's law is also used to refer to various generalizations of the law originally formulated by Ohm. The simplest example of this is:
Ohm's Law Formulas
Deriving values horizontally across columns is allowable as per the principles of series and parallel circuits:
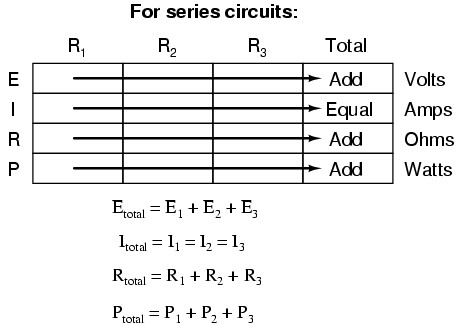

Subscribe to:
Posts (Atom)