logic gates
- is an idealized or physical device implementing a Boolean function; that is, it performs a logical operation on one or more logical inputs, and produces a single logical output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and unlimited fan-out, or it may refer to a non-ideal physical device .
Logic circuits include such devices as multiplexers, registers, arithmetic logic units (ALUs), and computer memory, all the way up through complete microprocessors, which may contain more than 100 million gates. In practice, the gates are made from field-effect transistors (FETs), particularly MOSFETs (metal–oxide–semiconductor field-effect transistors).
| Combination of Basic Logic Gates | ||||||||||||||||||||||||
| The OR, AND and NOT gates are the three basic circuits that make up all digital circuits. We shall discuss a few combinations of theses basic circuits. | ||||||||||||||||||||||||
|
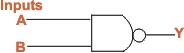
(I) NAND Gate: It is
combination of AND gate is connected to the input of a NOT
gate as shown in Fig. (a). Clearly, the output of a NAND gate
is opposite to the AND gate. This is illustrated in the truth
table for the NAND gate. Note that truth table for NAND gate
is developed by inverting the output of the AND gate.
The Boolean expression for NAND function is
This Boolean expression can
be read as Y = not A . B. TO perform
the Boolean algebra operation, First the input must be AND
and then the inversion is performed. Note that output from
NAND gate is always 1 excepted when all of the input are 1.Fig.
(b) shows the logic symbol for a NAND gate. The title bubble
(small circle) on the right end of the symbol means to invert
the AND.
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Truth
Table of NAND
|
||||||||||||||||||||||||
(II)
NOR Gate: It is a combination of OR gate and NOT gate.
In other words, output of OR gate is connected to the input
of a NOT gate as shown in Fig. (c). Note that output of OR
gate is inverted to form NOR gate. This is illustrated in
the truth table for NOR gate. It is clear that truth table
for NOR gate is developed by inverting the outputs of the
OR gate.
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Truth
Table of NOR
|
||||||||||||||||||||||||
|
The Boolean expression for
NOR function is:
The Boolean expression can
be read as Y = not A or B. To perform the Boolean algebra
operation, first the input must be OR and then inversion is
performed. Note that output from a NOR gate is high(1) only
when all the inputs are low (0). If any of the inputs are
high (1) the output is low (0). fig. (d) shows the logic symbol
for a NOR gate. The bubble (small circle) at the Y output
indicates inversion.
| ||||||||||||||||||||||||
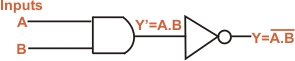
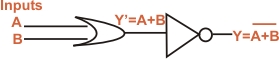
No comments:
Post a Comment